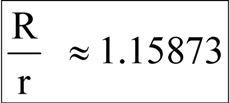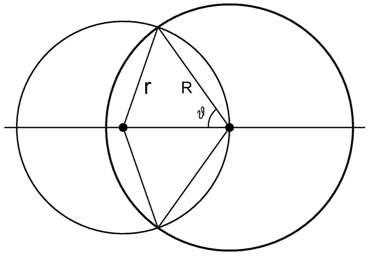
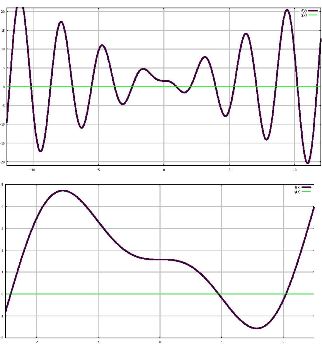
First we set up the geometry necessary to solve the "equal areas" problem. This geometry is shown in Fig. 1, to the right. The radius of the "fence" is small r and the radius of the "leash" is big R. The angle θ is measured from the horizontal axis to the intersection point of the two circles, as shown. The strategy will be to determine the value of θ necessary to make the intersection area equal to one-half the area of the smaller circle. Once we have θ we can easily determine the ratio R/r  using the relationship shown in Eq. 1. Eq. 2 shows the θ equation that meets the equal-areas condition. This cannot be solved analytically. We thus resort to numerical analysis. Fig. 3 is a plot of the left side of Eq. 2. The intersection of this curve with the 0 horizontal yields the result for θ that meets the condition of Eq. 2. We know that θ is less than 90 deg thus the proper solution for θ is shown in Eq. 3, below the plot. Our final result for R/r is shown in Eq. 4 below. This answer has been rounded off to 5 decimal places. As expected R/r  > 1. Fig. 3, below, shows the geometric solution with the proper proportions.

TO SEE OR DOWNLOAD A DETAILED DERIVATION OF THE THIS SOLUTION CLICK HERE: COMPLETE SOLUTION